3.4-3 消失點到底在哪裡？ Where Should We Put The Vanish Point ?

在前一篇文章中提到，徒手畫透視圖對於透視的概念必須有相當的瞭解，才能畫出符合透視邏輯的透視圖。

其中最為重要的觀念，就是「消失點」(Vanish Point)，簡稱V.P.。

當我們徒手畫透視圖時，必須先決定消失點的適當位置，這個透視圖才畫得下去。

而圖學的標準作法則是完成時消失點自然會出現在正確的位置，我們不需事先知道。

所以說，「消失點到底應該擺在哪裡？」就是徒手畫透視圖時最重要的問題。

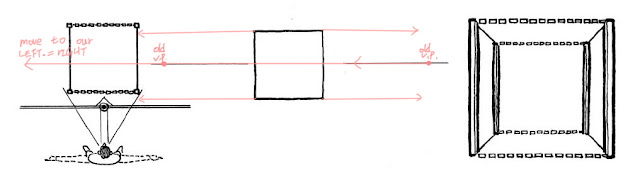
首先我們先來瞭解何謂「視線方向」與「視線平面」？

側視圖中的紅色箭頭就是我們的視線方向(View Direction)，假設將這個視線方向水平旋轉一圈就會得到一個平面，這個平面我們把它叫做「視線平面」(View Plane)。

視線平面本身是一個假想的平面，而且是一個無限大的平面，這個觀念請務必記住！

在透視圖中這個視線平面看起來會是一個水平線，就像右側的圖中一樣。

而中心點打叉（×）處就是我們的視線方向，因為視線方向永遠朝向正前方，所以在透視圖中畫不出來。

而視線平面所形成的水平線在透視圖中，也永遠會在畫面的正中央。

像下面的圖中一樣～

再來我們要說明當物體方向改變時，消失點會如何移動。

簡單的說，「物體方向往哪邊移動，這個方向的消失點就往哪邊移動。」

請看下面的範例說明～(平行四邊形有兩個方向，但是這裡我們先看其中的一組方向，另一組先不管。）

圖中的平面慢慢的往「上方」旋轉，而各自的消失點也慢慢的往「上方」移動。

當平面的方向慢慢旋轉到與視線方向成垂直的角度時(圖4)，消失點不知道跑到哪裡去了。

請再看另一個說明～

圖中的平面漸漸的轉向「右方」，而各自的消失點也往「右方」移動。

而圖4的方向與視線方向垂直時，消失點跟上一個範例一樣，不知道跑哪裡去了。

這個問題留到後面再討論。

我們再看下面的範例～

假設我們把圖中的方塊往左側旋轉，這兩個消失點會像下面一樣移動～

再繼續轉～

消失點又不知道跑到哪裡去了！

在這裡我們先做一個結論～「物體方向往哪邊移動，這個方向的消失點就往哪邊移動。」

就像下面的動畫示範一樣～

然後我們再來說明當物體方向與我們的視線方向垂直時，消失點到底在哪裡。

請記住，真實世界是一個無限大的三度空間，當物體方向與視線方向垂直時（左右垂直或上下垂直），消失點的位置其實就在我們視線的垂直方向無限遠處。

當消失點位於無限遠處時，通往這個消失點的直線自然也變成了平行線。

左圖中所有平面的A方向在上視圖中可以輕易看出與視線方向垂直，所以A方向的消失點就在視線正右方無限遠處。　　　　　　　　　　　因此通往這個消失點的直線都成了平行線。　　　　　　　　　　　　　　　　　　　　而圖中所有平面的B方向在平面1與平面5的情況，在側視圖中可以看出剛好與視線方向垂直，這時平面1與平面5的B方向消失點就在視線方向正上方與正下方無限遠處。　　　　　　　　　　　　　　　　平面3的B方向的消失點剛好就在視線的正前方，所以消失點位置就是打×的位置。　　　　　　　　　　　　　　也就是與視線方向相同。

因此得到一個重要的結論，當某個方向與視線方向呈現垂直時，該方向的消失點就在無限遠處。

而通往這個消失點的所有直線，必然會是平行線。

請注意，總共會有兩種垂直的情況發生，一個是在側視圖中與視線方向上下垂直，另一個是在上視圖中與視線方向左右垂直。

下面圖中劃上紅色的邊，方向剛好與視線垂直，所以呈現互相平行。

而另外兩組方向也是各自相同的方向，因此各自通往同一個消失點。

一般的透視法教材都是將透視區分為～一點透視、兩點透視、三點透視來分別討論。

但是一旦我們瞭解到當方向與視線相互垂直的時候，消失點的位置以及透視圖的模樣會如何變化。

這時我們不再需要將透視圖區分為～一點、兩點、三點透視來理解，因為實際上所有的透視圖全部都是－－「三點透視圖」。

更進一步的說，透視只有一種～就叫做「透視」。

在無限遠處的消失點雖然畫不出來，但是不代表不存在。

再來我們說明一下當方向旋轉同樣的角度時，消失點會如何移動。

當圖中的A方向往上方旋轉某個角度成為B方向時，消失點也往上方移動某個距離。

當B方向再一次往上方旋轉相同角度成為C方向時，消失點也會再往上方移動一樣的距離。

也就是說，當方向旋轉時，我們可以用消失點移動的距離來判斷旋轉的角度大小。

上圖中的火車每一節車廂的方向變化，就與各自的消失點之間的距離比例一樣。

而右側的三棟房子，左右兩棟的消失點與中間那棟的消失點的距離一樣，因此左右兩棟房子的方向與中間房子的方向是對稱的。

下圖中劃上紅色的那三頁，可以從消失點的相對距離看出彼此的方向在角度上是對稱的。

以上這篇文章中所提到的觀念，都是我們徒手畫透視圖時必須知道的重點。

無論如何，請務必確實理解它們。

後續的文章中還會繼續深入討論下去。

←Last Page          Next Page→